Στο σχήμα εμφανίζονται οι δυνάμεις που ασκούνται στο σώμα. Αναλύουμε το βάρος σε δύο συνιστώσες, την Βx στη διεύθυνση του νήματος και την Βy σε κάθετη διεύθυνση. Για τα μέτρα των δύο συνιστωσών έχουμε:Βx= Β·ημθ=mgσυνθ και Βy=mg·ημθ
α) Η κεντρομόλος επιτάχυνση είναι ίση:
ακ= υ2/R = 4m/s2.
β) ΣFR=mακ ή Τ-Βx =mακ ή Τ= mgσυνθ + mακ
Τ=(2·10·1/2+2·4)Ν=18Ν.
γ) Στην διεύθυνση την κάθετη προς το νήμα έχουμε:
ΣFy=mαy ή
.
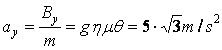Η επιτάχυνση αυτή έχει την διεύθυνση της εφαπτομένης στην κυκλική τροχιά, έχει δηλαδή την διεύθυνση της γραμμικής ταχύτητας και αλλάζει το μέτρο της (σε αντίθεση η κεντρομόλος επιτάχυνση αλλάζει την διεύθυνση της ταχύτητας). Έτσι ο ρυθμός μεταβολής του μέτρου της ταχύτητας είναι:
.
