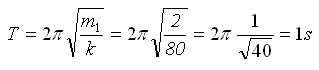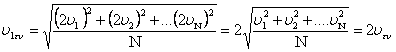Ερώτηση στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση.

Η κλίση στο διάγραμμα x-t μας δίνει την στιγμιαία ταχύτητα. Οπότε για t=1s είναι θετική, άρα το σώμα κινείται προς τα δεξιά, ενώ τη στιγμή t=2s το σώμα σταματά στιγμιαία (υ=0) πριν κινηθεί προς τ’ αριστερά. Η μετατόπιση είναι Δx= x_τ-x_α. Έτσι οι απαντήσεις είναι:

1. Την χρονική στιγμή t=1s το κινητό κινείται προς τα δεξιά. Σ
2. Την χρονική στιγμή t=2s το κινητό έχει μηδενική ταχύτητα. Σ
3. Η μετατόπισή του τη στιγμή t=4s είναι μηδέν. Σ
4. Η μετατόπισή του από t=2s έως t=4s είναι -10m. Σ

Πληροφορίες από το διάγραμμα θέσης-χρόνου.

1. Η κλίση στο διάγραμμα x-t είναι αριθμητικά ίση με την στιγμιαία ταχύτητα. Έτσι η κλίση στην θέση Α είναι -10m/s, στο Β είναι 0 και στο σημείο Γ είναι ίση με+10m/s.
2. Στο διάγραμμα α-t το εμβαδόν είναι αριθμητικά ίσο με την μεταβολή της ταχύτητας του κινητου.
   

Πραγματικά Ε= β·υ= 10·2 = 20m², ενώ

Δυ= υ_τ-υ_α = +10m/s- (-10m/s) = + 20m/s.

Διάγραμμα θέσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση.

1. Από 0-5s: Δx= -5m-20m= -25m
Από 0-10s: Δx= 20m-20m =0
2. Η εξίσωση κίνησης του κινητού είναι:

Δx= υ₀·t + ½ αt² (1)

Με αντικατάσταση t=5s και Δx=-25m στην (1) παίρνουμε:

-25= 5υ₀ + ½ α·5² ή
5υ₀+ 12,5 α= -25 (2)

Θέτοντας t=10 και Δx=0 στην (1) έχουμε:

0= 10·υ₀ + ½ α·10² ή
10υ₀ + 50α = 0 (3)

Πολλαπλασιάζουμε την (2) επί -2 και παίρνουμε:

-10υ₀ - 25α= 50 (4)

Προσθέτουμε τις (3) και (4) κατά μέλη και έχουμε:

25 α = 50 → α= 2m/s².

Με αντικατάσταση στην (3) έχουμε:

10υ₀ + 50·2 = 0 → υ₀= - 10m/s

Τα διαγράμματα είναι τα παρακάτω.

Μπορείτε να κατεβάσετε την απάντηση σε pdf.

Δύο μεταβολές αερίων.

Ένα αέριο βρίσκεται σε κατάσταση Α, σε δοχείο που κλείνεται με έμβολο. Κρατώντας σταθερή την θέση του εμβόλου, προσφέρουμε θερμότητα στο αέριο ίση με 200J, ερχόμενο σε κατάσταση Β. Κατόπιν αφήνουμε το έμβολο να κινηθεί μέχρι το αέριο να αποκτήσει την αρχική του θερμοκρασία (κατάσταση Γ), ενώ καλύψαμε τα τοιχώματα, ώστε να μην επιτρέψουμε διαρροή θερμότητας.

1)Να σχεδιάστε τις μεταβολές σε άξονες Ρ-V.

2)Ποιες προτάσεις είναι σωστές και ποιες λάθος:

• Κατά την μεταβολή ΑΒ το αέριο παράγει έργο. Λ
• Κατά την μεταβολή ΑΒ αυξάνεται η εσωτερική ενέργεια του αερίου κατά 200J. Σ
• Κατά την μεταβολή ΒΓ το αέριο αποβάλλει ενέργεια μέσω έργου. Σ
• Κατά την μεταβολή ΒΓ μειώνεται η εσωτερική ενέργεια κατά 200J. Σ
• Το αέριο παράγει έργο 200J κατά τη διάρκεια της μεταβολής ΒΓ. Σ

3) Ποιοι νόμοι περιγράφουν τις παραπάνω μεταβολές;
Η ΑΒ είναι ισόχωρη θέρμανση που περιγράφεται από το νόμο του Charles p/Τ= σταθ_, ενώ η ΒΓ είναι μια αδιαβατική εκτόνωση, νόμος poisson p·V^γ= σταθ.

Μεταβολές αερίων και 1ος Θερμοδυναμικός Νόμος.

Να συμπληρώσετε τα παρακάτω τετράγωνα, θέτοντας το πρόσημο (+) ή το (-) ή το μηδέν (0) ανάλογα με το τι συμβαίνει στις παρακάτω μεταβολές.

Μεταβολή	ΔV	ΔΡ	ΔΤ	W	ΔU	Q
Ισόθερμη εκτόνωση	+	-	0	+	0	+
Ισόχωρη ψύξη	0	-	-	0	-	-
Ισοβαρής θέρμανση	+	0	+	+	+	+
Αδιαβατική συμπίεση	-	+	+	-	+	0
Αδιαβατική εκτόνωση	+	-	-	+	-	0

.

Ενέργεια ιονισμού.

Ενθαλπία εξουδετέρωσης.

Για το ΗCl : n=CV=0,1.2mol= 0,2 mol

Για το Ca(OH)₂ : n=CV=0,2.1= 0,2mol.

Συνεπώς αντιδρούν 0,2mol Η⁺ με 0,2mol ΟΗ^-, οπότε ελευθερώνεται θερμότητα Q=0,2.57,1kj=11,42kj.

Η εξίσωση είναι:

2ΗCl_(αq) + Ca(OH)_2(αq) → CaCl_2(αq) + 2 H₂O­_(l) ΔH = - 114,2kj

Αφού η ΝΗ₃ είναι ασθενής βάση κατά την εξουδετέρωσή της από διάλυμα θα παραχθεί λιγότερη θερμότητα, αφού ένα μέρος της ενέργειας θα χρησιμοποιηθεί για να σπάσουν οι δεσμοί και να παραχθούν ιόντα.

Ενθαλπία

1. Η χημική ενέργεια 1mοl του Α είναι μικρότερη από την ενέργεια 1mοl του Γ. Σ
2. 1mοl Α και 1mοl Β έχουν τόση χημική ενέργεια, όση 1mοl Γ. Λ
3. Η αντίδραση είναι εξώθερμη. Λ
4. Η μεταβολή ΔΗ της αντίδρασης είναι θετική. Σ
5. Έχουμε ΔΗ=500kJ, οπότε q=-500kJ. Σ

Δομή ατόμου και ιόντων.

1) Με βάση τις αρχές δόμησης έχουμε:

1s², 2s², 2p⁶, 3s², 3p⁶, 4s², 3d⁹.

Αλλά όταν η υποστιβάδα d περιέχει 5 ηλεκτρόνια ή είναι συμπληρωμένη με 10 ηλεκτρόνια τότε το άτομο παρουσιάζει χαμηλότερη ενέργεια, οπότε έχουμε αυξημένη σταθερότητα, οπότε τελικά η κατανομή είναι:

1s², 2s², 2p⁶, 3s², 3p⁶, 3d¹⁰,4s¹.

2) Κάθε συμπληρωμένο τροχιακό έχει δύο ηλεκτρόνια με αντίθετο spin + ½ και – ½ . Εδώ τέτοια τροχιακά είναι τα 3s: 1s, 2s,3s, έξι τροχικά p, 2p, 3p και τα πέντε τροχιακά 3d. Έχουμε ακόμη ένα ηλεκτρόνιο στην 4s με spin + ½ . Άρα έχουμε 15 ηλεκτρόνια με spin + ½ .
3) Τα ιόντα προκύπτουν αφού αφαιρεθούν ηλεκτρόνια με την μεγαλύτερη ενέργεια. Έτσι η δομή των ιόντων είναι:

Cu⁺¹: 1s², 2s², 2p⁶, 3s², 3p⁶, 3d¹⁰.
Cu⁺²: 1s², 2s², 2p⁶, 3s², 3p⁶, 3d⁹.

Δυναμικό και δυναμικές γραμμές.

Σωστή πρόταση είναι η ii).

Δυναμικό και κίνηση φορτίου, μεταξύ δύο άλλων φορτίων.

1) Στο σχήμα έχουν σχεδιαστεί οι δυνάμεις που ασκούνται στο σωματίδιο στο σημείο Κ, όπου F₁ η απωστική δύναμη εξαιτίας του φορτίου q₁ και F₂ η αντίστοιχη από το q₂.

Από το νόμο του Coulomb έχουμε:

Για τη συνέχεια πατήστε ΕΔΩ.

Δυναμικό και κίνηση φορτίου.

1. Η δυναμική ενέργεια του φορτίου στο Α είναι U=q·V>0. Αν θα πήγαινε προς το Γ η δυναμική του ενέργεια θα αυξανόταν, πράγμα που δεν μπορεί να συμβεί, συνεπώς θα κινηθεί προς το Β που θα έχει μικρότερη δυναμική ενέργεια, αποκτώντας κινητική ενέργεια.
2. Στο σημείο Β έχει την ελάχιστη δυναμική ενέργεια και το σωματίδιο θα ισορροπήσει.
3. Το φορτίο –q έχει αρνητική δυναμική ενέργεια και θα κινηθεί προς σημεία με ακόμη πιο μικρή δυναμική ενέργεια, δηλαδή προς σημεία με μεγαλύτερο δυναμικό, άρα προς τα αριστερά.

Μια περισσότερο πρακτική εκδοχή της παραπάνω κατάστασης είναι η ανάρτηση:

Δυναμικό και κίνηση φορτίου, μεταξύ δύο άλλων φορτίων.

Διάγραμμα μετατόπισης.

1) Για την κίνηση από 0-6s έχουμε Δx₁=υ·Δt=8·6m=48m.
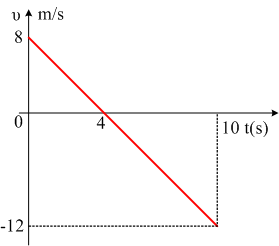
2) Για την ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση (επιβραδυνόμενη κίνηση) έχουμε:

υ=υ₀+α·Δt (1) και Δx₂=υ₀·Δt+ ½ α·Δt² (2)

Θέτοντας στην (1) υ=0 παίρνουμε:
0=8+(-2)·Δt → Δt=4s, δηλαδή το κινητό θα χρειαστεί χρονικό διάστημα 4s για να σταματήσει την χρονική στιγμή t₂=6s+4s=10s.
3) Με αντικατάσταση στην (2) έχουμε:
Δx₂=8·4+ ½ (-2)·4² = 32m-16m=16m, άρα θα φτάσει σε απόσταση Δx₁+Δx₂=48m+16m=64m από το σημείο Α.
4) Το διάγραμμα είναι το παρακάτω.

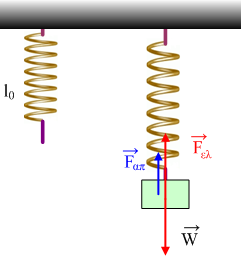
Φθίνουσα Ταλάντωση. Πόση ενέργεια "χάνουμε";

1) Θεωρώντας επίπεδο μηδενικής δυναμικής βαρυτικής ενέργειας το οριζόντιο επίπεδο που περνά από την θέση που το ελατήριο έχει μήκος 0,8m, έχουμε:

Ε_{Μηχ/αρχ}= mgh = 2·10·0,3J=6J.

Ενώ στην θέση που δίνεται:
Ε_{Μηχ/τελ}=Κ+U_ελ= ½ mυ²+ ½ kΔl²= ½ 2·0,8²J+ ½ 100·0,3²J=0,64J+4,5J=5,14J
Έτσι η ενέργεια που μετετράπη σε θερμότητα είναι Q=6-5,14=0,86J.
2) Οι δυνάμεις που ασκούνται στο σώμα φαίνονται στο σχήμα:
ΣF=ma → mg-kΔl-bυ=ma → b=(mg-kΔl-ma)/υ = (20-100·0,3-2·(-5,2))/0,8=0,5kg/s.
3) Ο ρυθμός με τον οποίο η ενέργεια ταλάντωσης μετατρέπεται σε θερμότητα είναι αντίθετος με την ισχύ της F_απ:
Ρ=F_απ·υ·συνα = -|F_απ|·|υ| = - bυ² = - 0,5·0,8²W= - 0,32 W,
Συνεπώς ο ζητούμενος ρυθμός είναι + 0,32J/s.

Ηλεκτρική Ταλάντωση. Ρυθμοί μεταβολής.

Αφού το αμπερόμετρο διαρρέεται από ρεύμα σταθερής έντασης, δεν έχουμε φαινόμενο αυτεπαγωγής στο πηνίο, οπότε Ε_αυτ=V_L=V_C=0, οπότε Q=CV=0 και από το νόμο του Ohm για κλειστό κύκλωμα παίρνουμε Ε=ΙR=5·2V= 10V.

Α) Η ενέργεια της ηλεκτρικής ταλάντωσης είναι Ε=U_Lmax= ½ LΙ²= ½ ·10·10^-3·5²J=125mJ.

Β) dq/dt=i=5Α/s, ενώ Ε_αυτ= - Ldi/dt → di/dt= - Ε_αυτ/L = 0 αφού τη στιγμή αυτή

Ε_αυτ=V_L=V_C=0.

Γ) Η ενέργεια ταλάντωσης παραμένει σταθερή, οπότε:

U_L+U_C=Ε_τ →

½ Li² + ½ q²/C = ½ LΙ² ή

U_C= ½ L(Ι²-i²) = ½ 10^-2·(25-9)= 0,08J.

Τη στιγμή αυτή αφού U_C= ½ CV² →

Αλλά τη στιγμή αυτή (για πρώτη φορά) ο πυκνωτής φορτίζεται (η πολικότητά του φαίνεται στο σχήμα), οπότε V_ΑΒ=400V και η ισχύς που απορροφά ο πυκνωτής είναι:

Ρ=V·i=400V·3 Α=1200W.

Σχόλιο: Αν θυμηθούμε λίγο τις αντιστοιχίες μεταξύ μηχανικής και ηλεκτρικής ταλάντωσης (x→q, υ→dq/dt=i, α→ di/dt). Συνεπώς για t=0 που η ένταση του ρεύματος είναι μέγιστη, ο ρυθμός μεταβολής της έντασης είναι μηδέν. Όπως ακριβώς στη θέση ισορροπίας η επιτάχυνση είναι μηδέν.

Φωτοβολία λαμπτήρα και συντονισμός.

Συνδέοντας μια δεύτερη αντίσταση R παράλληλα η ισοδύναμη αντίσταση R_ισ=R·R/2R =R/2 μειώνεται. Με βάση την καμπύλη συντονισμού, βλέπε σχήμα, αφού μικραίνει η αντίσταση R_ολ=R_ισ+R_Λ, αυξάνεται το πλάτος της έντασης, συνεπώς η φωτοβολία του λαμπτήρα αυξάνεται.

Κίνηση φορτισμένου σωματιδίου σε ομογενές ηλεκτρικό πεδίο.

Εφαρμόζουμε το Θ.Μ.Κ.Ε. μεταξύ των σημείων Α και Β.

Κ_τελ-Κ_αρχ= W_ΑΒ → 0- ½ mυ₀² = q(V_Α-V_Β) →

V_Α-V_Β= - ½ mυ₀²/q και με αντικατάσταση:

V_Α-V_Β= - ½ 2·10^-6·100²/(-0,01·10^-6) = 10^-4/10^-8V= 10⁴ V.

Ε=V/l = 10⁴/2·10^-2 V/m = 5·10⁵V/m.

Ο ρυθμός μεταβολής της ταχύτητας είναι η επιτάχυνση του σωματιδίου.

α= F/m = Ε·q/m = 5·10⁵·10^-8/2·10^-6 m/s²= 2,5·10³m/s².

Εφαρμόζουμε το Θ.Μ.Κ.Ε. μεταξύ της θέσης Α, όταν ξεκινά και της ίδιας θέσης όταν το σωματίδιο επιστρέφει:

Κ_τελ-Κ_αρχ= W_ΑΑ → ½ mυ² - ½ mυ₀² = q(V_Α-V_Α) =0 →
|υ|=|υ₀|=100m/s

Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση.

Η κίνηση του κινητού είναι ευθύγραμμη ομαλά μεταβαλλόμενη όπου έχουμε:

Δx= υ₀t+ ½ α·t² ή

x-x₀= υ₀t+ ½ α·t² και με αντικατάσταση:

0-20=8·10+ ½ α·100 →
α= - 2m/s².

Η ταχύτητα δίνεται από την σχέση υ=υ₀+αt και θέτοντας t=10s βρίσκουμε:

υ= 8+(-2)·10 = -12m/s.

Ενώ το σώμα σταματά την προς τα δεξιά του κίνηση, αλλάζοντας φορά κίνησης τη στιγμή που υ=0 και με αντικατάσταση:

υ=υ₀+αt → 0=8+(-2)t₂ → t₂=4s.

Τη στιγμή t₂ το σώμα έχει μετατοπισθεί κατά Δx= υ₀·t₂+ ½ α·t₂² = 8·4+ ½ (-2)·16 =16m.

Δx= υ₀t+ ½ α·t² = 8t+ ½ (-2)·t² = 8·t-t².

Ενώ για t=10s έχουμε: Δx= =20m
Η μετατόπιση είναι Δx=x-x₀ → x=x₀+Δx → x=20 +8t-t².
Οπότε με βάση αυτά οι γραφικές παραστάσεις είναι:

1ος Θερμοδυναμικός Νόμος και ενεργός ταχύτητα.

Το έργο είναι αριθμητικά ίσο με το εμβαδόν του γκριζαρισμένου τραπεζίου, δηλαδή:

W=(Β+β)·υ/2= (1+3)·10⁵·4·10^-3/2J= 800J.

Η μεταβολή της εσωτερικής ενέργειας είναι:
ΔU=U_Β-U_Α= 3/2 nRΤ_Β- 3/2 RΤ_Α= 3/2 (p_ΒV_Β-p_ΑV_Α) = 3/2 (1800-200)J= 2400 J.
Από τον 1^ο Θερμοδυναμικό νόμο παίρνουμε:

Q=ΔU+W = 800J+2400J=3200J.

2) Από την καταστατική εξίσωση έχουμε:
p_ΑV_Α = nRΤ_Α και p_ΒV_Β= nRΤ_Β και με διαίρεση κατά μέλη παίρνουμε:

Τ_Β/Τ_Α= (p_ΒV_Β/ p_ΑV_Α)= 1800/200= 9 → Τ_Β= 9 Τ_Α.

Αλλά U_Β= 3/2 nRΤ_Β = 3/2 nR9Τ_Α= 9U_Α, οπότε:

ΔU= 2400J

9U_Α-U_Α= 2400J → 8U_Α= 2400 → U_Α= 300J.

Έργο και θερμότητα σε ευθύγραμμη μεταβολή.

1) Λάθος. Η εσωτερική ενέργεια εξαρτάται μόνο από τη θερμοκρασία και η μεταβολή της εξαρτάται μόνο από τη μεταβολή της θερμοκρασίας. Έτσι ΔU_ευθ=ΔU_ισ=0.

2) Σωστό. Το έργο κατά τη διάρκεια της ευθύγραμμης είναι μεγαλύτερο από το έργο της ισόθερμης, αφού το εμβαδόν του σχηματιζόμενου χωρίου είναι μεγαλύτερο.

Αλλά Q_ευθ=ΔU+W_ευθ, ενώ Q_ισοθ= ΔU+W_ισοθ άρα Q_ευθ>Q_ισοθ.

Διάγραμμα ταχύτητας για δύο κινητά.

1) Για το Α κινητό:α₁=Δυ/Δt = (4-2)/(4-0) m/s²= 0,5m/s².

Για το Β κινητό: α₂=Δυ/Δt = (7-8)/(4-0) m/s²= - 0,25m/s².
2) Για t₁= 3s έχουμε:

υ₁= υ₀+α₁t₁= (2+0,5·3) m/s = 3,5 m/s και
υ₂= υ₀ + α₂t₁= 8 + (-0,25·3) = 7,25m/s.

3) Τη στιγμή που τα κινητά έχουν ίσες ταχύτητες υ₁=υ₂ →

υ₀₁+α₁t = υ₀₂+ α₂t →
2+0,5t = 8+(-0,25t) ή
2+0,5t = 8-0,25t ή
0,75t = 6 ή
t=8s.
Ενώ υ= υ₀₁+α₁t= 2+0,5·8= 6m/s.

4) Για t=8s τα δύο κινητά έχουμε μετατοπισθεί κατά:

Δx₁= (2+6)·8/2m=32m, ενώ
Δx₂= (8+6)·8/2= 56m.

Προφανώς προηγείται το Β κινητό κατά 56m-32m= 24m.
5) Το Β κινητό αλλάζει φορά κίνησης τη στγμή που υ_Β=0

υ₀₂+ α₂t=0 ή
8-0,25t=0 ή
t₂ = 32s.

Κίνηση δύο κινητών. Μελέτη διαγραμμάτων.

1) Από 0-4s: α₁=Δυ/Δt = 8/4m/s²= 2m/s², ενώ από 4s-6s: α₂=Δυ/Δt = (10-8)/(6-4) m/s²= 1m/s².

2) Από 0-4s η ταχύτητα του Α κινητού δίνεται από την εξίσωση:

υ₁= α₁·t₁ = 2·3,4 m/s = 6,8 m/s.

Για το χρονικό διάστημα μετά από τα 4s έχουμε:

υ₂= υ₀+α₂·(t-t₀) όπου υ₀=υ₄=8m/s και t₀=4s. Έτσι:

υ₂=8m/s + 1·(5,2-4)m/s= 9,2m/s.

3) Έχουμε υ₃= υ₀+α₂·(t₃ -t₀) → 8,3 = 8 +1·(t₃-4) → t₃=4,3s.

4) Η μετατόπισή του από 4s-6s είναι αριθμητικά ίση με το εμβαδόν του σχηματιζόμενου τραπεζίου: Δx= (Β+β)·υ/2 = (10+8)·2/2= 18m.

5) Για t=6s: Οι ταχύτητες είναι ίσες υ_Α=υ_Β=10m/s, Το Β έχει μεγαλύτερη επιτάχυνση (η ευθεία έχει μεγαλύτερη κλίση, ενώ το Α έχει μετατοπισθεί περισσότερο αφού το σχηματιζόμενο χωρίο έχει μεγαλύτερο εμβαδόν.

Test. ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ.

Στη θέση ισορροπίας ΣF=0 → F_ελ-w=0 → kΔl=m₁g→ k=m₁g/Δl=80Ν/m.
Παίρνουμε το σώμα σε μια τυχαία θέση που απέχει κατά x από τη θέση ισορροπίας:
ΣF= w-F_ελ=m₁g-k(Δl+x) = m₁g-kΔl – kx = -kx συνεπώς το σώμα εκτελεί α.α.τ. με D=k.

Ε= ½ kΑ² όπου Α=d η αρχική απομάκρυνση

Ε= ½ ·80·0,4²J = 6,4 J.

Αφού η κρούση γίνεται μετά από χρόνο t₁=0,5s=Τ/2 το σώμα Σ βρίσκεται στην πάνω ακραία θέση της τροχιάς του έχοντας μηδενική ταχύτητα.
Η σφαίρα πέφτει ελεύθερα, οπότε:
υ₂= gt= 5m/s και

y= ½ gt²= ½ ·10·0,5²m = 1,25m

Κατά συνέπεια h=y+A = 1,25+0,4=1,655m.

Εφαρμόζουμε την ΑΔΟ για την κρούση:

Και θεωρώντας την προς τα κάτω φορά ως θετική παίρνουμε:

m₂·υ₂ +0= - m₂υ₂^΄ + m₁·υ₁ →

υ₁= 0,5·(5+3)/2 = 2m/s.

Οπότε η νέα ενέργεια ταλάντωσης είναι:
Ε= ½ kx² + ½ m₁υ₁² = 6,4J+ ½ ·2·4 J= 10,4J.

J

Μη αντιστρεπτή μεταβολή αερίου.

1) W_ΑΒ=0 αφού ο όγκος παραμένει σταθερός.

Το έργο κατά τη διάρκεια της ΒΓ είναι αριθμητικά ίσο με το εμβαδόν του τραπεζίου:

W_ΒΓ= - (Β+β)·υ/2= - (1+4)·10⁵·6·10^-3/2 J= -1500J.

Ο όγκος μειώνεται και γι’ αυτό το έργο είναι αρνητικό.

2) Το έργο κατά τη διάρκεια της μη αντιστρεπτής μεταβολής δεν μπορεί να υπολογιστεί από εμβαδόν. Το μόνο που μπορούμε να ξέρουμε είναι ότι είναι μικρότερο από το αντίστοιχο έργο της αντιστρεπτής.

3( Εδώ δηλαδή, αν το αέριο πήγαινε αντιστρεπτά (ισοβαρή θέρμανση) από το Γ→Α το έργο θα ήταν:

W_ισ= pΔV = 4·6·10²J= 2400J.

Συνεπώς το έργο στην μη αντιστρεπτή μπορεί να είναι W_ΓΑ=2200J.

Έργο κατά την μετακίνηση φορτίου.

1. Το φορτίο q₃ έλκεται από το q₁, οπότε για να ισορροπεί πρέπει να έλκεται και από το q₂ με μια δύναμη ίσου μέτρου, συνεπώς και το q₂ είναι θετικό με τιμή q₂=+2μC.
2. Το δυναμικό στο σημείο Μ είναι:

V_Μ= kq₁/r₁ + kq₂/r₂.
Αλλά q₁=q₂ και r₁=r₂=α/2, οπότε:
V_Μ= 2kq₁/(α/2) = 2·9·10⁹·2·10^-6/10^-2 V= 36·10⁵V.
Άρα U_Μ=q₃·V_Μ= (-10^-6)·36·10⁵J = -3,6J.

3) Εφαρμόζουμε το Θ.Μ.Κ.Ε. από το Μ στην κορυφή Α:

Κ_Α-Κ_Μ = W_Fηλ+ W_Fεξ (1)
Αλλά Κ_Α-Κ_Μ=0 ενώ W_Fηλ= q₃·(V_Μ-V_Α) (2)

Αλλά V_Α = kq₁/α + kq₂/α = 2·kq₁/α = 2·9·10⁹·2·10^-6/2·10^-2 V= 18·10⁵V και από την σχέση (2) παίρνουμε:

W_Fηλ= q₃·(V_Μ-V_Α) = -1·10^-6·(36·10⁵-18·10⁵)= - 1,8J

Και η (1) δίνει:

0-0=1,8J+ W_Fεξ → W_Fεξ= + 1,8J.

Δυναμικό και ενέργεια.

1) Το σωματίδιο στο σημείο Α θα έχει δυναμική ενέργεια U=9·10^-4J, όση είναι δηλαδή η ενέργεια που δώσαμε στο σωματίδιο.

Αλλά V_Α=U_Α/q = 9·10^-4J/(-1·10^-6C) = - 900V.

2) Αφού το σωματίδιο κινείται προς το Β, την ίδια κατεύθυνση έχει και η δύναμη και αντίθετη κατεύθυνση θα έχει η ένταση, μιας και το υπόθεμα είναι αρνητικό.

3) Εφαρμόζουμε το Θ.Μ.Κ.Ε. από το Α μέχρι το Β.

Κ_Β-Κ_Α = W_ΑΒ → W_ΑΒ= ½ mυ₁² →

W_ΑΒ= ½ mυ₁²= ½ ·4·10^-6·10² J = 2·10^-4J.

Ισχύει: V_Α-V_Β= W_ΑΒ/q →

V_Β= V_Α – W_ΑΒ/q = -900V- 2·10^-4/(-10^-6)V = -900V+200V= -700V.

4) Το σωματίδιο θα επιταχύνεται μέχρι να φτάσει στο άπειρο, όπου η δυναμική του ενέργεια θα μηδενιστεί, συνεπώς εκεί η κινητική του ενέργεια θα είναι μέγιστη Κ_max= 9·10^-4J.

΄Η με άλλα λόγια η δύναμη που δέχεται το σωματίδιο από το πεδό είναι συντηρητική, οπότε η μηχανική ενέργεια παραμένει σταθερή:

Κ_Α+U_Α= Κ_∞ + U_∞ και αφού Κ_Α=U_∞= 0 →

Κ _∞= 9·10^-4J.

Σταθερές επιταχύνσεις κινητών.

1. Θέτουμε x=0 την αρχική θέση και t₀=0 τη χρονική στιγμή που ξεκινούν τα δύο οχήματα. Για όσο χρόνο επιταχύνεται το Ι.Χ. ισχύει:

υ₁= α₁t₁(1)και x₁= ½ α₁t₁²(2).

Από την (1)t₁= υ₁/α₁ = (108·1000/3600)/2 s = 30/2 s = 15s

Οπότε το Ι.Χ. βρίσκεται στη θέση x₁= ½ ·2·15²m = 225 m.

Μετά συνεχίζει για χρονικό διάστημα 5s και μετατοπίζεται κατά:

Δx₁=υ₁·Δt₁= 30·5m=150m.

Οπότε το (Α) όχημα έχει φτάσει στη θέση x₂=x₁+Δx₁=375m.

Έτσι τη χρονική στιγμή t₂=t₁+Δt = 15s+5s = 20s τα δύο οχήματα είναι δίπλα-δίπλα.
2) Μέχρι τη στιγμή t₂ το Β όχημα έχει διανύσει απόσταση x₂= 375m, οπότε:

x₂= ½ α₂t₂² → α₂= 2x₂/t₂² = 2·375/400 m/s²= 1,875m/s².

3) υ₂= α₂·t₂= 1,875·20 m/s= 37,5m/s.

Ένταση ηλεκτρικού πεδίου και δυναμικές γραμμές.

Η ένταση στο Μ είναι διπλάσια της Ε₁ και όχι μηδέν.

Στο σημείο Γ υπάρχει ΕΝΑ πεδίο, μια συνισταμένη ένταση και περνά μια δυναμική γραμμή.
Η ολική έντασαη στο Γ προκύπτει με τη μέθοδο του παραλληλογράμμου και δεν είναι ίση με (5+4) Ν/C.

Ε_Β=k|q₁|/r² → q₁=E·r²/k ή
q₁= 10⁷·3²·10^-4/9·10⁹ = 10^-6C = 1μC.
F₂=Ε_Β·|q₂| = 10⁷·10^-6Ν = 10Ν.

Test: Ένταση Ηλεκτρικού πεδίου και δυναμικές γραμμές.

….
…α) Στο σημείο Α υπάρχει πεδίο που οφείλεται στο φορτίο q. Λ

…… β) Η κίνηση του σωματιδίου από το Α στο Β είναι ευθύγραμμη ομαλή. Λ

…… γ) Η κίνηση του σωματιδίου από το Α στο Β είναι ευθύγραμμη ομαλά επιταχυνόμενη. Λ

…… δ) Αν το σωματίδιο Σ είχε διπλάσιο φορτίο (-2q), τότε η ένταση του πεδίου στο Α θα ήταν διπλάσια. Λ

Η ένταση στο σημείο Α οφείλεται στο φορτίο Q (πηγή) και όχι στο q.

Ε=k|Q|/r² →

r²= k |Q|/E = 9·10⁹· 4·10^-6/10⁷ = 36·10^-4m² →

r= 0,06m.

F=E|q| = 10⁷·10^-6N = 10N.

Διαφορά φάσης και πλάτος.

α) x= x₁+x₂= 2ημ100πt + 2ημ104πt →

x= 4 συν2πt·ημ102πt.

β) Για τη χρονική στιγμή t₁= 0,5s:

1) φ₁= 100πt = 100π·0,5rad = 50π rad

φ₂= 104πt = 104π·0,5 rad = 52π rad

Οπότε Δφ = 2π rad

Το πλάτος της ταλάντωσης είναι:

Α= |4·συν2πt| = |4·συνπ| = 4m.

2) Για την στιγμή t₂= 1,25s έχουμε:

φ₁= 100πt = 100π·1,25rad = 125π rad

φ₂= 104πt = 104π·1,25 rad = 130π rad.

Δφ= φ₂-φ₁= 5π.

Για το πλάτος:

Α= |4·συν2πt| = |4·συν2π·1,25| = |4·συν2,5π| = 0

Υπάρχει σχόλιο;;

Σύνθεση Ταλαντώσεων. Προσοχή στην φάση.

Τα πλάτη είναι Α₁=8·3 ^½ cm, A₂= 16cm.

f₁= f₂= ω/2π = 3π/2π Ηz = 1,5 Ηz.

Η απομάκρυνση της δεύτερης ταλάντωσης γράφεται:
y₂= 16 συν (3πt+π/3) = 16 ημ(3πt + π/3 + π/2) = 16 ημ (3πt + 5π/6), οπότε η διαφορά φάσης μεταξύ των δύο ταλαντώσεων είναι:

φ= 3πt + 5π/6 – 3πt = 5π/6 rad.

Η συνισταμένη κίνηση έχει εξίσωση:
y= A ημ(3πt+θ), όπου:

και

Αφού δεν ορίζεται η εφαπτομένη τότε θ=π/2 (προφανώς η γωνία θ παίρνει τιμή μεταξύ 0 και 5π/6.

Άρα y= 8 ημ(3πt + π/2) cm.

Τη στιγμή t₁=2s έχουμε:
y₁=8ημ(6π+π/2) =8cm.
Προφανώς υ=0, ενώ α= - ω²·y= 9π²·8cm/s² = 7,2m/s².

Νόμος Coulomb – Ένταση.

Στο σχήμα φαίνεται η δύναμη F που ασκείται μεταξύ δύο φορτίων.

1. Αν το ένα φορτίο είναι αρνητικό τότε το άλλο φορτίο θα είναι σίγουρα …Αρνητικό……………………….
   
2. Αν το ένα φορτίο είναι θετικό τότε το άλλο φορτίο θα είναι σίγουρα ……θετικό……………
3. Aν το φορτίο Q₁ αντικατασταθεί με φορτίο ίσο με 2Q₁ τότε η δύναμη F θα ……διπλασιαστεί……………………..
4. Αν η απόσταση r γίνει 2r τότε η δύναμη F θα …υποτετραπλασιαστεί…………..
5. Aν το φορτίο Q₁ αντικατασταθεί με φορτίο ίσο με 2Q₁ και η απόσταση r γίνει 2r τότε η δύναμη F θα ………υποδιπλασιαστεί…………………..
6. Αν το φορτίο Q₁ = 10μC και το Q₂ = 40μC και η απόσταση r είναι 3cm να βρείτε τη δύναμη F.
   Δίνεται :

.
F=kQ₁·Q₂/r² = 9·10⁹·10·10^-6·40·10^-6/9·10^-4 N = 4·10⁵N.

Σύνθεση Ταλαντώσεων. Προσοχή στην φάση.

Οι εξισώσεις γράφονται:

y₁=0,2·συν10t = 0,2·ημ(10t+ π/2)

y₂= 0,2·3 ^½ ημ10t (S.Ι.)

Οπότε:

Ενώ

Συνεπώς θ=π/6.
Προσέξτε ποιο πλάτος θα βάλουμε στον αριθμητή και ποιο στον παρονομαστή….
Δείτε και τα περιστρεφόμενα διανύσματα τη χρονική στιγμή t=0

Έτσι η εξίσωση της κίνησης είναι:

y= 0,4·ημ(10t+ π/6) (S.Ι.)

Η ταχύτητα του σώματoς είναι:
υ=Αωσυν(ωt+θ) = 4 συν(10π/12+π/6)=4 συνπ= - 4m/s

Ταχύτητες μορίων και θερμοκρασία-πίεση.

Η ενεργός ταχύτητα των μορίων υπολογίζεται από την εξίσωση:

Αν διπλασιαστούν όλες οι ταχύτητες θα έχουμε:

Αρχικά Κ_μ= ½ mυ_εν²

Τελικά Κ_1μ = ½ mυ_1εν²

Με διαίρεση κατά μέλη παίρνουμε:

Κ_1μ/Κ_μ= υ_1εν²/υ_εν² = 4 → Κ_μ1=4Κ_μ.

Αρχικά ½ mυ_εν² = 3/2 kΤ

Και ½ mυ_1εν² = 3/2 kΤ₁

Με διαίρεση κατά μέλη παίρνουμε:

Τ₁/Τ = υ_1εν²/υ_εν² = 4 → Τ₁= 4Τ

Από την εξίσωση p= 2/3 (Ν/V)·Κ_μ συμπεραίνουμε ότι όταν τετραπλασιαστεί η μέση κινητική ενέργεια θα τετραπλασιαστεί και η πίεση.

Γραφικές παραστάσεις μετατόπισης και διαστήματος.

1) Η κλίση της ευθείας είναι σταθερή, συνεπώς σε όλο το χρονικό διάστημα το κινητό έχει σταθερή επιτάχυνση:

α= Δυ/Δt = (0-30)/(6-0) m/s = - 5m/s² .

2) υ= υ₀+αt = 30m/s + (-5)m/s²·10s= - 20 m/s.

3) Το εμβαδόν του σχηματιζόμενου χωρίου είναι αριθμητικά ίσο με την μετατόπιση, οπότε μέχρι τη στιγμή t₂=6s το κινητό έχει μετατοπισθεί κατά:

Δx₁= ½ ·6·30 m = 90 m.

Ενώ από 6s-10s:

Δx₂= - ½ 4·20 m = - 40m
( αφού το εμβαδόν είναι κάτω από τον άξονα, η αντίστοιχη μετατόπιση είναι αρνητική).

Οπότε η συνολική μετατόπιση είναι Δx= Δx₁+Δx₂= 90m-40m = 50m.
Λαμβάνοντας εξάλλου την την εξίσωση της μετατόπισης έχουμε:

Δx= υ₀t + ½ α·t²

Όπου η επιτάχυνση α είναι αρνητική. Συνεπώς η γραφική παράσταση είναι παραβολή με τα κοίλα προς τα κάτω και το διάγραμμα είναι το παρακάτω:

Το αντίστοιχο διάγραμμα του διαστήματος είναι εξάλλου το παρακάτω.

Σχόλιο για συναδέλφους: Ποιο από τα δύο διαγράμματα θα πρέπει να ζητάμε από τους μαθητές μας; Κοιτάζοντας τις ασκήσεις του σχολικού βιβλίου, μιλάει συνεχώς για διάγραμμα διαστήματος - χρόνου. Μήπως πρέπει να αντικαταστήσουμε τη λέξη «διάστημα» με την λέξη « μετατόπιση»;