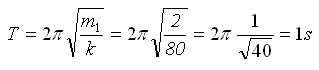Test. ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ.

Στη θέση ισορροπίας ΣF=0 → F_ελ-w=0 → kΔl=m₁g→ k=m₁g/Δl=80Ν/m.
Παίρνουμε το σώμα σε μια τυχαία θέση που απέχει κατά x από τη θέση ισορροπίας:
ΣF= w-F_ελ=m₁g-k(Δl+x) = m₁g-kΔl – kx = -kx συνεπώς το σώμα εκτελεί α.α.τ. με D=k.

Ε= ½ kΑ² όπου Α=d η αρχική απομάκρυνση

Ε= ½ ·80·0,4²J = 6,4 J.

Αφού η κρούση γίνεται μετά από χρόνο t₁=0,5s=Τ/2 το σώμα Σ βρίσκεται στην πάνω ακραία θέση της τροχιάς του έχοντας μηδενική ταχύτητα.
Η σφαίρα πέφτει ελεύθερα, οπότε:
υ₂= gt= 5m/s και

y= ½ gt²= ½ ·10·0,5²m = 1,25m

Κατά συνέπεια h=y+A = 1,25+0,4=1,655m.

Εφαρμόζουμε την ΑΔΟ για την κρούση:

Και θεωρώντας την προς τα κάτω φορά ως θετική παίρνουμε:

m₂·υ₂ +0= - m₂υ₂^΄ + m₁·υ₁ →

υ₁= 0,5·(5+3)/2 = 2m/s.

Οπότε η νέα ενέργεια ταλάντωσης είναι:
Ε= ½ kx² + ½ m₁υ₁² = 6,4J+ ½ ·2·4 J= 10,4J.

J