
i) Από την αρχή διατήρησης της ενέργειας ανάμεσα στην αρχική θέση και στην βάση του επιπέδου, θεωρώντας σαν επίπεδο μηδενικής δυναμικής ενέργειας το οριζόντιο επίπεδο που περνά από το κέντρο Ο του κυλίνδρου, έχουμε:
Κ1+U1 = Κ2 + U2
mgh= ½ mυ02 ή
υ02 =2gh =900m2/s2
υ0= 30m/s
ii) Στο οριζόντιο επίπεδο ασκείται στον κύλινδρο τριβή ολίσθησης μέτρου:
Τ=μΝ= μmg= 40Ν
Εφαρμόζοντας τον θεμελιώδη νόμο της μηχανικής για την μεταφορική και για την στροφική κίνηση του κυλίνδρου παίρνουμε:
ΣFx= mαcm από όπου αcm = 1m/s2 με φορά προς τα αριστερά.
Στ=Ιαγων ή
ΤR= ½ mR2 αγων
αγων =2Τ/mR= 4rad/s2.
Ο κύλινδρος εκτελεί ομαλά επιβραδυνόμενη μεταφορική κίνηση για την οποία:
υcm= υ0-αcmt (1) και x= υ0t- ½ αcmt2 (2)
και στροφική ομαλά επιταχυνόμενη με εξισώσεις:
ω= αγωνt (3) και θ= ½ αγωνt2 (4)
Μέχρι πότε θα συμβαίνει αυτό; Μέχρι την στιγμή που ένα σημείο Α επαφής του κυλίνδρου, με το έδαφος να αποκτήσει μηδενική ταχύτητα. Δηλαδή μέχρι τη στιγμή που υcm=υγρ, όπως στο σχήμα.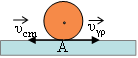
Με την βοήθεια των (1) και (3) θα έχουμε:
υ0- αcmt = (αγωνt)·R από όπου
t=υ0/(αcm+αγωνR) = 10s
Άρα υcm=υ0-αcmt =30m/s-1·10m/s= 20m/s
και ω= αγωνt =40rad/s.
Από τις εξισώσεις (2) και (4) βρίσκουμε:
x= υ0t- ½ αcmt2 = 30·10m- ½ 1·100m= 250m
θ= ½ 4·100rad =200rad.
Άρα για τα έργα έχουμε:
WΤ= -Τx = - 40·250J=-10000J
Wτ= + τ·θ= ΤRθ= 40· ½ ·200J= 4000J.
Με βάση τα παραπάνω συμπεραίνουμε ότι η τριβή αφαιρεί μεταφορική κινητική ενέργεια 10.000J από τον κύλινδρο, από τα οποία τα 4000J τα μετατρέπει σε περιστροφική κινητική ενέργεια. Τα υπόλοιπα; Τα υπόλοιπα 6000J μετατρέπονται σε θερμότητα.
Σχόλιο:
Κατά την περιστροφή του κυλίνδρου ήρθαν σε επαφή με το έδαφος τα σημεία της περιφέρειάς του μήκους Δs=θ·R= 200· ½ m = 100m, συνεπώς ο κύλινδρος γλίστρησε κατά:
x1= x-Δs= 250m-100m = 150m
Εξαιτίας αυτής της ολίσθησης παράγεται θερμότητα:
Q= |Τ·x1| = 40·150J= 6000J.


